BOJ 25945 - 컨테이너 재배치 (Python3)

상당히 최근에 올라온 문제다. 아마 1주일도 안 되었을 것이다.

그래도 이 문제를 푸는 데 필요한 직관이 생각보다는 중요할 것 같아서 글을 쓰게 되었다.

나만 이렇게 생각했나 했는데 다들 이런 방법으로 풀더라.

 

그럼 본격적으로 풀이에 돌입해 보자.

---

문제

항구의 컨테이너 하치장 바닥에는 컨테이너를 쌓을 수 있는 칸이 일렬로 총 n개가 그려져 있고, 현재 하치장에는 총 m개의 컨테이너가 쌓여 있다. 개별 컨테이너의 높이는 모두 1로 동일하며, 각 칸에 쌓을 수 있는 컨테이너의 개수에는 제한이 없다. 즉, \(a_i\) (1 ≤ i ≤ n)가 현재 i번째 칸에 쌓여있는 컨테이너의 개수를 나타내면, \(m = \sum_{i=1}^{n}{a_i}\)의 관계가 만족된다.

현재와 같이 높이에 아무 제한이 없이 컨테이너가 쌓여 있을 경우 각 칸별로 쌓여있는 컨테이너의 개수의 차이가 심하여 안전상 문제점을 유발할 수 있기 때문에, 일부 컨테이너를 크레인을 이용하여 다른 칸으로 옮겨서 각 칸의 높이 차이가 1이하가 되도록 재배치하고자 한다. 즉, 임의의 i, j에 대해 \(\left| a_i - a_j \right| ≤ \) 이 만족되어야 한다. 컨테이너는 한번에 한 개씩만 옮길 수 있고 옮기는 거리에 따른 추가 비용은 없다고 가정한다.

예를 들어 <그림 1>과 같이 35개의 컨테이너가 8개의 칸에 쌓여 있을 경우 m = 35, n = 8에해당한다. 이를 높이 차이가 1 이하가 되도록 재배치하면 <그림 2>와 같은 결과를 얻을 수 있고, 이 경우 5개의 컨테이너를 옮겨야 한다.

[그림 1]　　[그림 2]

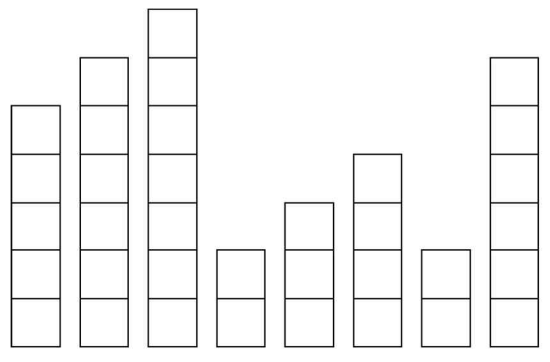
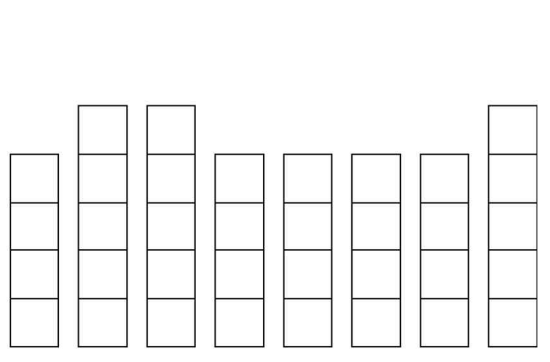
입력으로 각 칸에 초기에 쌓여 있는 컨테이너의 높이 \(a_1, a_2, \cdots , a_n\)이 주어질 때, 임의의 i, j에 대해 \(\left| a_i - a_j \right| ≤ 1\) 조건을 만족하기 위해 옮겨야 하는 컨테이너의 최소 개수를 출력하는 프로그램을 작성하시오.

 

입력

입력은 표준입력을 사용한다. 첫 번째 줄에 컨테이너를 쌓을 수 있는 칸의 개수를 나타내는 양의 정수 n (1 ≤ n ≤ \(10^6\))이 주어진다. 다음 줄에는 현재 각 칸에 쌓여 있는 컨테이너의 개수 \(a_i\)를 나타내는 n개의 0 이상의 정수들이 주어지고, 컨테이너의 총 개수 m 은 1 ≤ m ≤ \(2 \times 10^9\) 으로 제한한다

 

예제 입력)

# 예제 입력 1
4
1 2 3 3

# 예제 입력 2
8
5 6 7 2 3 4 2 6

 

출력

출력은 표준출력을 사용한다. 문제의 조건을 만족하기 위해 옮겨야 하는 컨테이너의 최소 개수를 한 줄에 출력한다.

 

예제 출력)

# 예제 출력 1
1

# 예제 출력 2
5

 

---

내 코드

n, cnt1, cnt2 = int(input()), 0, 0
l = list(map(int, input().split()))
avg = sum(l) // n
for i in l:
    if i > avg+1: cnt1 += (i-avg-1)
    elif i < avg: cnt2 += (avg-i)
    
print(max(cnt1, cnt2))

 

문제 조건에 너무 겁을 먹지 마라.

임의의 i, j에 대해 \(\left| a_i - a_j \right| ≤ 1\) 조건을 만족한다는 의미는, 아무거나 두 개를 집었을 때 기껏해야 하나 차이가 난다는 뜻이다!

그렇다면 재배치 후 i번째 칸에 쌓여 있는 컨테이너 개수를 \(b_i\)로 두면 어떤 정수 x이 존재하여, 임의의 i에 대해서 \(b_i=x, x+1)이 성립한다는 것이다. (단, 모든 컨테이너가 x+1만큼 쌓여 있지는 않는다고 치자.)

그러면 간단한 부등식 하나가 만들어지는데, 이는 다음과 같다.

\[nx=\sum_{i=1}^{n}x\le\sum_{i=1}^{n}b_i=\sum_{i=1}^{n}a_i=m<\sum_{i=1}^{n}(x+1)=n(x+1)\]

줄이면? \(nx\le m<n(x+1)\)이 된다. 이는 x=m//n과 완전히 같게 된다!

 

그럼 이제 <그림 3>을 통해서 한 번 보자. 예제 그림을 살짝 매만진 것이다.

예제에는 35개의 컨테이너와 8개의 줄이 있고, 따라서 여기서는 x=4가 된다. 이를 파란 줄로, x+1을 빨간 줄로 표기했다.

<그림 3>

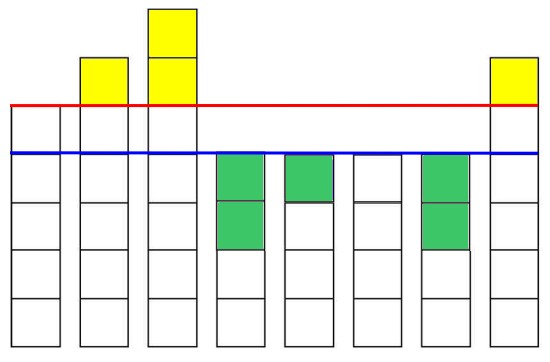
노란색 컨테이너는 빨간 선을 초과했으니까 어딘가로 옮겨서 낮춰야 하는 양이고, 초록색 빈 공간은 파란 선에도 못 미치니 어디선가 컨테이너를 찾아와서 채워야 하는 양이다.

그렇다면 노란색의 총 수와 초록색의 총 수 중 더 큰 쪽만 찾아서 출력하면 될 일이다. 만약 노란색 컨테이너가 남는다면 임의의 x 높이를 가진 컨테이너 줄에 올려버리면 되고, 초록색 빈 공간이 남는다면 임의의 x+1 높이를 가진 컨터이너 줄에서 하나를 가져와서 채우면 될 테니 말이다.

cnt1, cnt2를 각각 노란색 컨테이너, 초록색 빈 공간의 총량을 세는 변수로 지정한 다음, \(a_i\)가 x+1보다 크면 cnt1에 초과분인 \(a_i-x-1\)을 더하고, x보다 작으면 cnt2에 미달분인 \(x-a_i\)을 더하면 된다.

마지막에 그 둘을 비교한 다음 더 큰 값을 출력하면 끝.

 

이로서 25945번의 풀이를 마친다.

그럼, 오늘도 당신의 코딩 실력이 상승하기를.